domov Dermatologija Kako pomnožiti število z različnimi predznaki. Množenje števil z različnimi predznaki (6. razred)

Kako pomnožiti število z različnimi predznaki. Množenje števil z različnimi predznaki (6. razred)

V tem članku se bomo ukvarjali z množenje števil z različnimi predznaki. Tu bomo najprej oblikovali pravilo množenja pozitivnih in negativnih števil, ga utemeljili, nato pa razmislili o uporabi tega pravila pri reševanju primerov.

Navigacija po strani.

Pravilo za množenje števil z različnimi predznaki

Množenje pozitivnega števila z negativnim številom, pa tudi negativnega števila s pozitivnim številom, se izvede na naslednji način: pravilo množenja števil z različnimi predznaki: če želite pomnožiti števila z različnimi predznaki, morate pomnožiti in pred nastalim produktom postaviti znak minus.

Zapišimo to pravilo v črkovni obliki. Za vsako pozitivno realno število a in vsako negativno realno število −b velja enakost a·(−b)=−(|a|·|b|) , in tudi za negativno število −a in pozitivno število b enakost (−a)·b=−(|a|·|b|) .

Pravilo za množenje števil z različnimi znaki je popolnoma skladno z lastnosti operacij z realnimi števili. Dejansko je na njihovi podlagi enostavno pokazati, da za realna in pozitivna števila a in b obstaja veriga enakosti oblike a·(−b)+a·b=a·((−b)+b)=a·0=0, kar dokazuje, da sta a·(−b) in a·b nasprotni števili, kar implicira enakost a·(−b)=−(a·b) . In iz tega sledi veljavnost obravnavanega pravila množenja.

Upoštevati je treba, da navedeno pravilo za množenje števil z različnimi predznaki velja tako za realna števila kot za racionalna števila in za cela števila. To izhaja iz dejstva, da imajo operacije z racionalnimi in celimi števili enake lastnosti, kot so bile uporabljene v zgornjem dokazu.

Jasno je, da se množenje števil z različnimi predznaki po dobljenem pravilu zmanjša na množenje pozitivnih števil.

Pretehtamo le primere uporabe razstavljenega pravila množenja pri množenju števil z različnimi znaki.

Primeri množenja števil z različnimi predznaki

Poglejmo si več rešitev primeri množenja števil z različnimi predznaki. Začnimo s preprostim primerom, da se osredotočimo na korake pravila in ne na računsko zapletenost.

Pomnožite negativno število −4 s pozitivnim številom 5.

Po pravilu za množenje števil z različnimi predznaki moramo najprej pomnožiti absolutne vrednosti prvotnih faktorjev. Modul −4 je 4, modul 5 pa 5 in če pomnožimo naravni števili 4 in 5, dobimo 20. Na koncu ostane še, da pred nastalo številko postavimo znak minus, imamo −20. S tem je množenje končano.

Na kratko lahko rešitev zapišemo takole: (−4)·5=−(4·5)=−20.

(−4)·5=−20.

Pri množenju ulomkov z različnimi predznaki je treba znati množiti navadne ulomke, množiti decimalke in njihove kombinacije z naravnimi in mešanimi števili.

Pomnožite števila z različnimi predznaki 0, (2) in.

Ko smo izvedli pretvorbo periodičnega decimalnega ulomka v navadni ulomek in izvedli tudi prehod iz mešanega števila v nepravilni ulomek, bomo iz prvotnega produkta prišli do produkta navadnih ulomkov z različnimi znaki oblike . Ta produkt je enak pravilu za množenje števil z različnimi predznaki. Vse, kar ostane, je, da pomnožimo navadne ulomke v oklepajih, ki jih imamo .

Ločeno je treba omeniti množenje števil z različnimi predznaki, ko sta eden ali oba faktorja

Zdaj pa se ukvarjajmo s množenje in deljenje.

Recimo, da moramo +3 pomnožiti z -4. Kako narediti?

Razmislimo o takem primeru. Trije ljudje so se zadolžili in vsak je imel 4 dolarje dolgov. Kolikšen je skupni dolg? Da bi ga našli, morate sešteti vse tri dolgove: 4 dolarje + 4 dolarje + 4 dolarje = 12 dolarjev. Odločili smo se, da seštevek treh številk 4 označimo kot 3x4. Ker v tem primeru govorimo o dolgu, je pred 4 znak "-". Vemo, da je skupni dolg 12 $, zato je naš problem zdaj 3x(-4)=-12.

Enak rezultat bomo dobili, če ima v skladu s problemom vsaka od štirih oseb dolg 3 $. Z drugimi besedami, (+4)x(-3)=-12. In ker vrstni red faktorjev ni pomemben, dobimo (-4)x(+3)=-12 in (+4)x(-3)=-12.

Povzemimo rezultate. Ko pomnožite eno pozitivno število in eno negativno število, bo rezultat vedno negativno število. Številčna vrednost odgovora bo enaka kot v primeru pozitivnih števil. Zmnožek (+4)x(+3)=+12. Prisotnost znaka »-« vpliva samo na znak, ne pa na številčno vrednost.

Kako pomnožiti dve negativni števili?

Na žalost je na to temo zelo težko najti primeren primer iz resničnega življenja. Zlahka si je predstavljati dolg v višini 3 ali 4 dolarjev, popolnoma nemogoče pa si je predstavljati -4 ali -3 ljudi, ki so se zadolžili.

Morda bomo šli drugače. Pri množenju, ko se predznak enega od faktorjev spremeni, se predznak produkta spremeni. Če spremenimo predznaka obeh faktorjev, moramo spremeniti dvakrat delovna oznaka, najprej iz pozitivnega v negativno, nato pa obratno, iz negativnega v pozitivno, to pomeni, da bo izdelek imel začetni predznak.

Zato je povsem logično, čeprav malo čudno, da je (-3) x (-4) = +12.

Položaj znaka ko se pomnoži, se spremeni takole:

pozitivno število x pozitivno število = pozitivno število;
negativno število x pozitivno število = negativno število;
pozitivno število x negativno število = negativno število;
negativno število x negativno število = pozitivno število.

Z drugimi besedami, če pomnožimo dve števili z enakimi predznaki, dobimo pozitivno število. Če pomnožimo dve števili z različnimi predznaki, dobimo negativno število.

Enako pravilo velja za dejanje, ki je nasprotno množenju – za.

To lahko preprosto preverite tako, da zaženete inverzne operacije množenja. Če v vsakem od zgornjih primerov pomnožite količnik z deliteljem, boste dobili dividendo in se prepričajte, da ima enak predznak, na primer (-3)x(-4)=(+12).

Ker prihaja zima, je čas, da razmislite, v kaj preobuti čevlje svojega železnega konja, da ne bi zdrsnil na ledu in se počutil samozavestnega na zimskih cestah. Pnevmatike Yokohama lahko na primer kupite na spletni strani: mvo.ru ali kakšni drugi, glavna stvar je, da so visoke kakovosti, več informacij in cene najdete na spletni strani Mvo.ru.

Ta članek nudi podroben pregled deljenje števil z različnimi predznaki. Najprej je podano pravilo za deljenje števil z različnimi predznaki. Spodaj so primeri deljenja pozitivnih števil z negativnimi in negativnih števil s pozitivnimi.

Navigacija po strani.

Pravilo za deljenje števil z različnimi predznaki

Pri članku deljenje celih števil je bilo pridobljeno pravilo za deljenje celih števil z različnimi predznaki. Razširimo ga lahko na racionalna in realna števila, če ponovimo vse sklepanje iz zgornjega članka.

Torej, pravilo za deljenje števil z različnimi predznaki ima naslednjo formulacijo: če želite pozitivno število deliti z negativnim ali negativno število s pozitivnim, morate dividendo deliti z modulom delitelja in pred dobljeno številko postaviti znak minus.

Zapišimo to pravilo delitve s črkami. Če imata števili a in b različna predznaka, je formula veljavna a:b=−|a|:|b| .

Iz navedenega pravila je razvidno, da je rezultat deljenja števil z različnimi predznaki negativno število. Ker sta modul dividende in modul delitelja pozitivni števili, je njun količnik pozitivno število, znak minus pa naredi to število negativno.

Upoštevajte, da obravnavano pravilo reducira deljenje števil z različnimi predznaki na deljenje pozitivnih števil.

Lahko podate še eno formulacijo pravila za deljenje števil z različnimi predznaki: če želite število a deliti s številom b, morate število a pomnožiti s številom b −1, inverznim številom b. to je a:b=a b −1 .

To pravilo je mogoče uporabiti, ko je mogoče preseči množico celih števil (ker nima vsako celo število inverza). Z drugimi besedami, velja tako za niz racionalnih števil kot tudi za niz realnih števil.

Jasno je, da vam to pravilo za deljenje števil z različnimi predznaki omogoča prehod od deljenja k množenju.

Enako pravilo se uporablja pri deljenju negativnih števil.

Še vedno je treba razmisliti, kako se to pravilo za deljenje števil z različnimi znaki uporablja pri reševanju primerov.

Primeri deljenja števil z različnimi predznaki

Razmislimo o rešitvah več značilnosti primeri deljenja števil z različnimi predznaki razumeti načelo uporabe pravil iz prejšnjega odstavka.

Negativno število −35 delite s pozitivnim številom 7.

Pravilo za deljenje števil z različnimi predznaki predpisuje najprej iskanje modulov dividende in delitelja. Modul −35 je 35, modul 7 pa 7. Zdaj moramo modul dividende deliti z modulom delitelja, to je, da moramo 35 deliti s 7. Če se spomnimo, kako poteka deljenje naravnih števil, dobimo 35:7=5. Zadnji preostali korak v pravilu deljenja števil z različnimi predznaki je, da pred dobljeno številko postavimo minus, imamo −5.

Tukaj je celotna rešitev: .

Izhajati je bilo mogoče iz drugačne formulacije pravila za deljenje števil z različnimi znaki. V tem primeru najprej poiščemo inverz delitelja 7. To število je navadni ulomek 1/7. Tako,. Ostaja še pomnožiti števila z različnimi predznaki: . Očitno smo prišli do enakega rezultata.

(−35):7=−5 .

Izračunaj količnik 8:(−60) .

Po pravilu za deljenje števil z različnimi predznaki imamo 8:(−60)=−(|8|:|−60|)=−(8:60) . Dobljeni izraz ustreza negativnemu navadnemu ulomku (glejte znak deljenja kot ulomkovo vrstico), ulomek lahko zmanjšate za 4, dobimo .

Na kratko zapišimo celotno rešitev: .

Pri deljenju ulomkov racionalnih števil z različnimi predznaki sta njihov delitelj in delitelj običajno predstavljena kot navadni ulomki. To je posledica dejstva, da ni vedno priročno izvajati deljenja s številkami v drugem zapisu (na primer v decimalnem).

Modul dividende je enak, modul delitelja pa 0,(23) . Če želite deliti modul dividende z modulom delitelja, pojdimo na navadne ulomke.

Ta lekcija pokriva množenje in deljenje racionalnih števil.

Vsebina lekcije

Množenje racionalnih števil

Pravila za množenje celih števil veljajo tudi za racionalna števila. Z drugimi besedami, za množenje racionalnih števil morate biti sposobni

Prav tako morate poznati osnovne zakonitosti množenja, kot so: komutativni zakon množenja, asociativni zakon množenja, distribucijski zakon množenja in množenja z nič.

Primer 1. Poiščite vrednost izraza

To je množenje racionalnih števil z različnimi predznaki. Če želite pomnožiti racionalna števila z različnimi predznaki, morate pomnožiti njihove module in pred nastalim odgovorom postaviti minus.

Da bi jasno videli, da imamo opravka s števili z različnimi predznaki, damo vsako racionalno število v oklepaj skupaj z njegovimi predznaki.

Modul števila je enak , modul števila pa je enak . Ko smo dobljene module pomnožili kot pozitivne ulomke, smo prejeli odgovor, vendar smo pred odgovorom postavili minus, kot je od nas zahtevalo pravilo. Da bi zagotovili ta minus pred odgovorom, je bilo množenje modulov izvedeno v oklepaju, pred katerim je bil minus.

Kratka rešitev izgleda takole:

Primer 2. Poiščite vrednost izraza

Primer 3. Poiščite vrednost izraza

To je množenje negativnih racionalnih števil. Če želite pomnožiti negativna racionalna števila, morate pomnožiti njihove module in dati plus pred rezultatom

Rešitev tega primera lahko na kratko zapišemo:

Primer 4. Poiščite vrednost izraza

Rešitev tega primera lahko na kratko zapišemo:

Primer 5. Poiščite vrednost izraza

To je množenje racionalnih števil z različnimi predznaki. Pomnožimo module teh števil in pred dobljeni odgovor postavimo minus

Kratka rešitev bo videti veliko preprostejša:

Primer 6. Poiščite vrednost izraza

Pretvorimo mešano število v nepravi ulomek. Ostalo napišemo tako, kot je

Dobili smo množenje racionalnih števil z različnimi predznaki. Pomnožimo module teh števil in pred dobljeni odgovor postavimo minus. Vnos z moduli lahko preskočimo, da ne zamašimo izraza

Rešitev tega primera lahko zapišemo na kratko

Primer 7. Poiščite vrednost izraza

To je množenje racionalnih števil z različnimi predznaki. Pomnožimo module teh števil in pred dobljeni odgovor postavimo minus

Sprva se je izkazalo, da je odgovor nepravi ulomek, vendar smo v njem izpostavili cel del. Upoštevajte, da je celoštevilski del ločen od modula ulomkov. Nastalo mešano število je bilo v oklepaju, pred katerim je bil znak minus. To se naredi, da se zagotovi, da je zahteva pravila izpolnjena. In pravilo je zahtevalo, da je pred prejetim odgovorom minus.

Rešitev tega primera lahko na kratko zapišemo:

Primer 8. Poiščite vrednost izraza

Najprej pomnožimo in in pomnožimo dobljeno število s preostalim številom 5. Vnos z moduli bomo preskočili, da ne bomo zmešali izraza.

odgovor: vrednost izraza je enako −2.

Primer 9. Poiščite pomen izraza:

Pretvorimo mešana števila v nepravilne ulomke:

Dobili smo množenje negativnih racionalnih števil. Pomnožimo module teh števil in pred dobljeni odgovor postavimo plus. Vnos z moduli lahko preskočimo, da ne zamašimo izraza

Primer 10. Poiščite vrednost izraza

Izraz je sestavljen iz več dejavnikov. V skladu z asociativnim zakonom množenja, če je izraz sestavljen iz več faktorjev, potem produkt ne bo odvisen od vrstnega reda dejanj. To nam omogoča, da dani izraz ocenimo v poljubnem vrstnem redu.

Ne izumljajmo kolesa znova, ampak izračunaj ta izraz od leve proti desni po vrstnem redu faktorjev. Preskočimo vnos z moduli, da ne zmedemo izraza

Tretje dejanje:

Četrto dejanje:

odgovor: vrednost izraza je

Primer 11. Poiščite vrednost izraza

Spomnimo se zakona množenja z nič. Ta zakon pravi, da je produkt enak nič, če je vsaj eden od faktorjev enak nič.

V našem primeru je eden od faktorjev enak nič, zato brez izgubljanja časa odgovorimo, da je vrednost izraza enaka nič:

Primer 12. Poiščite vrednost izraza

Produkt je enak nič, če je vsaj eden od faktorjev enak nič.

V našem primeru je eden od faktorjev enak nič, zato brez izgube časa odgovorimo, da je vrednost izraza enako nič:

Primer 13. Poiščite vrednost izraza

Uporabite lahko vrstni red dejanj in najprej izračunate izraz v oklepaju ter dobljeni odgovor pomnožite z ulomkom.

Uporabite lahko tudi distribucijski zakon množenja - vsak člen vsote pomnožite z ulomkom in dobljene rezultate seštejte. Uporabili bomo to metodo.

Glede na vrstni red operacij, če izraz vsebuje seštevanje in množenje, je treba najprej izvesti množenje. Zato v nastalem novem izrazu dajmo v oklepaje tiste parametre, ki jih je treba pomnožiti. Tako lahko jasno vidimo, katera dejanja izvesti prej in katera pozneje:

Tretje dejanje:

odgovor: vrednost izraza enako

Rešitev tega primera lahko zapišemo veliko krajše. Videti bo takole:

Jasno je, da je ta primer mogoče razrešiti tudi v mislih. Zato bi morali razviti veščino analiziranja izraza, preden ga rešite. Verjetno ga je mogoče rešiti mentalno in prihraniti veliko časa in živcev. In pri testih in izpitih je, kot veste, čas zelo dragocen.

Primer 14. Poiščite vrednost izraza −4,2 × 3,2

To je množenje racionalnih števil z različnimi predznaki. Pomnožimo module teh števil in pred dobljeni odgovor postavimo minus

Opazite, kako so bili pomnoženi moduli racionalnih števil. V tem primeru je bilo za množenje modulov racionalnih števil potrebno .

Primer 15. Poiščite vrednost izraza −0,15 × 4

To je množenje racionalnih števil z različnimi predznaki. Pomnožimo module teh števil in pred dobljeni odgovor postavimo minus

Opazite, kako so bili pomnoženi moduli racionalnih števil. V tem primeru je bilo za množenje modulov racionalnih števil potrebno znati.

Primer 16. Poiščite vrednost izraza −4,2 × (−7,5)

To je množenje negativnih racionalnih števil. Pomnožimo module teh števil in pred dobljeni odgovor postavimo plus

Deljenje racionalnih števil

Pravila za deljenje celih števil veljajo tudi za racionalna števila. Z drugimi besedami, da bi lahko delili racionalna števila, morate biti sposobni

Sicer pa se uporabljajo enake metode za deljenje navadnih in decimalnih ulomkov. Če želite navadni ulomek deliti z drugim ulomkom, morate prvi ulomek pomnožiti z recipročno vrednostjo drugega ulomka.

Če želite decimalni ulomek razdeliti na drug decimalni ulomek, morate premakniti decimalno vejico v dividendu in delitelju v desno za toliko števk, kolikor jih je za decimalno vejico v delitelju, nato pa izvesti deljenje kot pri redna številka.

Primer 1. Poiščite pomen izraza:

To je deljenje racionalnih števil z različnimi predznaki. Če želite izračunati tak izraz, morate prvi ulomek pomnožiti z recipročno vrednostjo drugega.

Torej, pomnožimo prvi ulomek z recipročno vrednostjo drugega.

Dobili smo množenje racionalnih števil z različnimi predznaki. In takšne izraze že znamo izračunati. Če želite to narediti, morate module teh racionalnih števil pomnožiti in pred nastalim odgovorom postaviti minus.

Dopolnimo ta primer do konca. Vnos z moduli lahko preskočimo, da ne zamašimo izraza

Torej je vrednost izraza

Podrobna rešitev je naslednja:

Kratka rešitev bi izgledala takole:

Primer 2. Poiščite vrednost izraza

To je deljenje racionalnih števil z različnimi predznaki. Če želite izračunati ta izraz, morate prvi ulomek pomnožiti z recipročno vrednostjo drugega.

Recipročna vrednost drugega ulomka je ulomek . Pomnožimo prvi ulomek z njim:

Kratka rešitev bi izgledala takole:

Primer 3. Poiščite vrednost izraza

To je deljenje negativnih racionalnih števil. Če želite izračunati ta izraz, morate znova pomnožiti prvi ulomek z recipročno vrednostjo drugega.

Recipročna vrednost drugega ulomka je ulomek . Pomnožimo prvi ulomek z njim:

Dobili smo množenje negativnih racionalnih števil. Že vemo, kako se izračuna tak izraz. Morate pomnožiti module racionalnih števil in dati plus pred dobljeni odgovor.

Dokončajmo ta primer do konca. Vnos z moduli lahko preskočite, da izraza ne zmešate:

Primer 4. Poiščite vrednost izraza

Za izračun tega izraza morate prvo število −3 pomnožiti z inverznim ulomkom od .

Inverzna stran ulomka je ulomek . Prvo število −3 pomnožimo z njim

Primer 6. Poiščite vrednost izraza

Če želite izračunati ta izraz, morate prvi ulomek pomnožiti z recipročno vrednostjo 4.

Recipročna vrednost števila 4 je ulomek. Pomnožite prvi ulomek z njim

Primer 5. Poiščite vrednost izraza

Če želite izračunati ta izraz, morate prvi ulomek pomnožiti z inverzno vrednostjo −3

Inverzna vrednost od −3 je ulomek. Pomnožimo prvi ulomek z njim:

Primer 6. Poiščite vrednost izraza −14,4 : 1,8

To je deljenje racionalnih števil z različnimi predznaki. Za izračun tega izraza morate modul dividende deliti z modulom delitelja in pred dobljenim odgovorom postaviti minus.

Opazite, kako je bil modul dividende deljen z modulom delitelja. V tem primeru je bilo treba biti sposoben, da bi to naredil pravilno.

Če se ne želite ukvarjati z decimalkami (in to se pogosto dogaja), potem te, nato te mešane številke pretvorite v nepravilne ulomke in nato izvedite samo deljenje.

Izračunajmo prejšnji izraz −14,4 : 1,8 na ta način. Pretvorimo decimalke v mešana števila:

Zdaj pa pretvorimo nastala mešana števila v nepravilne ulomke:

Zdaj lahko delite neposredno, namreč delite ulomek z ulomkom. Če želite to narediti, morate prvi ulomek pomnožiti z inverznim ulomkom drugega:

Primer 7. Poiščite vrednost izraza

Pretvorimo decimalni ulomek −2,06 v nepravi ulomek in ta ulomek pomnožimo z recipročno vrednostjo drugega ulomka:

Večnadstropni ulomki

Pogosto lahko naletite na izraz, v katerem je delitev ulomkov zapisana z ulomkovo črto. Na primer, izraz bi lahko zapisal takole:

Kakšna je razlika med izrazoma in? Prav nobene razlike ni. Ta dva izraza imata enak pomen in med njima lahko postavimo enačaj:

V prvem primeru je znak deljenja dvopičje, izraz pa je zapisan v eni vrstici. V drugem primeru je deljenje ulomkov zapisano z ulomkovo črto. Rezultat je delček, ki ga ljudje strinjajo, da ga kličejo večnadstropna.

Ko naletite na takšne večnadstropne izraze, morate uporabiti ista pravila za deljenje navadnih ulomkov. Prvi ulomek je treba pomnožiti z recipročno vrednostjo drugega.

Takšne ulomke je zelo neprijetno uporabljati v rešitvi, zato jih lahko zapišete v razumljivi obliki z dvopičjem in ne z ulomkom kot znakom deljenja.

Na primer, zapišimo večnadstropni ulomek v razumljivi obliki. Če želite to narediti, morate najprej ugotoviti, kje je prvi ulomek in kje drugi, ker tega ni vedno mogoče narediti pravilno. Večnadstropni ulomki imajo več ulomkov, ki lahko zmedejo. Glavna frakcijska črta, ki ločuje prvi ulomek od drugega, je običajno daljša od ostalih.

Po določitvi glavne ulomne črte lahko zlahka razumete, kje je prvi ulomek in kje je drugi:

Primer 2.

Poiščemo glavno ulomkovo črto (je najdaljša) in vidimo, da je celo število −3 deljeno z navadnim ulomkom

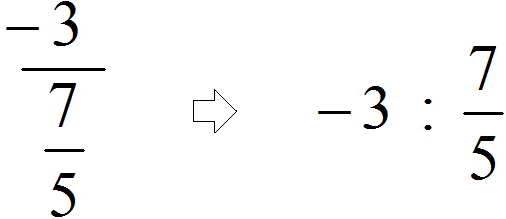
In če bi pomotoma vzeli drugo ulomkovo vrstico za glavno (tisto, ki je krajša), bi se izkazalo, da delimo ulomek s celim številom 5. V tem primeru, tudi če je ta izraz izračunan pravilno, problem bo nepravilno rešen, saj je dividenda v tem primeru število −3, delitelj pa ulomek.

Primer 3. Zapišimo večnivojski ulomek v razumljivi obliki

Poiščemo glavno ulomkovo črto (je najdaljša) in vidimo, da je ulomek deljen s celim številom 2

In če bi pomotoma vzeli prvo ulomkovo vrstico (tisto, ki je krajša), bi se izkazalo, da delimo celo število −5 z ulomkom. V tem primeru, tudi če je ta izraz pravilno izračunan, problem bo rešen nepravilno, saj je dividenda v tem primeru ulomek , delitelj pa celo število 2.

Kljub dejstvu, da je delo z večnivojskimi ulomki neprijetno, se bomo z njimi srečevali zelo pogosto, zlasti pri študiju višje matematike.

Seveda je za pretvorbo večnadstropnega ulomka v razumljivo obliko potreben dodaten čas in prostor. Zato lahko uporabite hitrejšo metodo. Ta metoda je priročna in izhod vam omogoča, da dobite že pripravljen izraz, v katerem je prvi ulomek že pomnožen z recipročnim ulomkom drugega.

Ta metoda se izvaja na naslednji način:

Če je frakcija na primer štirinadstropna, se številka, ki se nahaja v prvem nadstropju, dvigne v zgornje nadstropje. In figura, ki se nahaja v drugem nadstropju, se dvigne v tretje nadstropje. Dobljena števila morajo biti povezana z znaki za množenje (×).

Kot rezultat, mimo vmesnega zapisa, dobimo nov izraz, v katerem je prvi ulomek že pomnožen z recipročnim ulomkom drugega. Udobje in to je to!

Da bi se izognili napakam pri uporabi te metode, lahko upoštevate naslednje pravilo:

Od prvega do četrtega. Od drugega do tretjega.

Pravilo se nanaša na tla. Figuro iz prvega nadstropja je treba dvigniti v četrto nadstropje. In figuro iz drugega nadstropja je treba dvigniti v tretje nadstropje.

Poskusimo izračunati večnadstropni ulomek z uporabo zgornjega pravila.

Torej dvignemo številko, ki se nahaja v prvem nadstropju, v četrto nadstropje, številko, ki se nahaja v drugem nadstropju, dvignemo v tretje nadstropje.

Kot rezultat, mimo vmesnega zapisa, dobimo nov izraz, v katerem je prvi ulomek že pomnožen z recipročnim ulomkom drugega. Nato lahko uporabite svoje obstoječe znanje:

Poskusimo izračunati večnivojski ulomek z novo shemo.

Obstajajo samo prvo, drugo in četrto nadstropje. Tretjega nadstropja ni. Vendar ne odstopamo od osnovne sheme: figuro dvignemo iz prvega nadstropja v četrto nadstropje. In ker tretjega nadstropja ni, pustimo številko v drugem nadstropju takšno, kot je

Kot rezultat, mimo vmesnega zapisa, smo dobili nov izraz, v katerem je prvo število −3 že pomnoženo z recipročnim ulomkom drugega. Nato lahko uporabite svoje obstoječe znanje:

Poskusimo izračunati večnadstropni delež z uporabo nove sheme.

Obstajajo samo drugo, tretje in četrto nadstropje. Ni prvega nadstropja. Ker ni prvega nadstropja, se v četrto nadstropje ne moremo povzpeti, lahko pa figuro dvignemo iz drugega nadstropja v tretje:

Kot rezultat, mimo vmesnega zapisa, smo prejeli nov izraz, v katerem je bil prvi ulomek že pomnožen z obratno vrednostjo delitelja. Nato lahko uporabite svoje obstoječe znanje:

Uporaba spremenljivk

Če je izraz zapleten in se vam zdi, da vas bo zmedel v procesu reševanja problema, potem lahko del izraza vstavite v spremenljivko in nato delate s to spremenljivko.

Matematiki to pogosto počnejo. Kompleksen problem se razdeli na lažje podnaloge in reši. Nato se rešene podnaloge zberejo v eno samo celoto. To je ustvarjalen proces in človek se ga z leti nauči s trdim treningom.

Uporaba spremenljivk je upravičena pri delu z večnivojskimi ulomki. Na primer:

Poiščite vrednost izraza

Torej je ulomek v števcu in v imenovalcu katerega so ulomki. Z drugimi besedami, spet se soočamo z večnadstropno frakcijo, ki nam ni tako všeč.

Izraz v števcu lahko vnesete v spremenljivko s poljubnim imenom, na primer:

Toda v matematiki je v takem primeru običajno poimenovati spremenljivke z velikimi latiničnimi črkami. Ne prekinimo te tradicije in prvi izraz označimo z veliko črko A

In izraz v imenovalcu lahko označimo z veliko črko B

Zdaj ima naš prvotni izraz obliko . To pomeni, da smo številski izraz zamenjali s črkovnim, pri čemer smo predhodno v spremenljivki A in B vnesli števec in imenovalec.

Zdaj lahko ločeno izračunamo vrednosti spremenljivke A in vrednost spremenljivke B. Končane vrednosti bomo vstavili v izraz.

Poiščimo vrednost spremenljivke A

Poiščimo vrednost spremenljivke B

Zdaj zamenjajmo njihove vrednosti v glavni izraz namesto spremenljivk A in B:

Dobili smo večnadstropni ulomek, v katerem lahko uporabimo shemo "od prvega do četrtega, od drugega do tretjega", to je, da dvignemo številko v prvem nadstropju v četrto nadstropje in dvignemo številko, ki se nahaja v drugem nadstropju do tretjega nadstropja. Nadaljnji izračuni ne bodo težki:

Tako je vrednost izraza −1.

Seveda smo si ogledali zelo preprost primer, vendar je bil naš cilj naučiti se, kako lahko s spremenljivkami olajšamo stvari in zmanjšamo napake.

Upoštevajte tudi, da je rešitev za ta primer mogoče napisati brez uporabe spremenljivk. Izgledalo bo kot

Ta rešitev je hitrejša in krajša in v tem primeru je bolj smiselno, da jo zapišemo na ta način, če pa se izkaže, da je izraz kompleksen, sestavljen iz več parametrov, oklepajev, korenov in potenc, je priporočljivo, da ga izračunate v več stopenj, pri čemer del svojih izrazov vnese v spremenljivke.

Vam je bila lekcija všeč?
Pridružite se naši novi skupini VKontakte in začnite prejemati obvestila o novih lekcijah

Cilji lekcije:

Poučna:

oblikovanje pravil za množenje števil z enakimi in različnimi predznaki;
obvladovanje in izboljšanje spretnosti množenja števil z različnimi predznaki.

Izobraževalni:

razvoj miselnih operacij: primerjava, posploševanje, analiza, analogija;
razvoj veščin samostojnega dela;
širjenje obzorja učencev.

Poučna:

negovanje kulture vodenja evidenc;
vzgoja odgovornosti, pozornosti;
negovanje zanimanja za predmet.

Vrsta lekcije: učenje nove snovi.

Oprema: računalnik, multimedijski projektor, kartice za igro "Matematični boj", testi, kartice znanja.

Plakati na stenah:

Znanje je najodličnejša lastnina. Vsak si prizadeva za to, a ne pride samo od sebe.
Al-Biruni
V vsem želim priti do samega bistva...
B. Pasternak

Učni načrt

Med poukom

I. Organizacijski trenutek

pripravljenost učencev na pouk.

II. Učiteljev uvodni govor

Fantje, danes smo se z vami srečali ne zaman, ampak za plodno delo: pridobivanje znanja.

Odkar vesolje obstaja,
Ni ga, ki ne potrebuje znanja.
Ne glede na jezik in starost, ki jo izberemo,
Človek že od nekdaj teži k znanju...
Rudaki

Med poukom bomo preučevali novo snov, jo utrjevali, delali samostojno, ocenjevali sebe in svoje tovariše. Vsak ima na mizi kartonček znanja, v katerem je naša lekcija razdeljena na stopnje. Na to kartico boste vnesli točke, ki jih boste pridobili na različnih stopnjah lekcije. In na koncu lekcije bomo povzeli. Te kartice postavite na vidno mesto.

III. Ustno delo (v obliki igre "Matematični boj")

Fantje, preden preidemo na novo temo, ponovimo, kaj smo se prej naučili. Vsak ima na mizi list papirja z igro "Matematični boj". V navpičnih in vodoravnih stolpcih so številke, ki jih je treba dodati. Te številke so označene s pikami. Odgovore bomo zapisali v tiste celice na polju, kjer so pike.

Tri minute za dokončanje. Začeli smo z delom.

Zdaj sva dela izmenjala s sosedom po mizi in jih med seboj preverjala. Če menite, da odgovor ni pravilen, ga previdno prečrtajte in zraven napišite pravilnega. Preverimo.

Zdaj pa preverimo odgovore z zaslonom ( Pravilni odgovori so projicirani na platno).

Za pravilno rešeno

5 nalog se oceni s 5 točkami;
4 naloge – 4 točke;
3 naloge – 3 točke;
2 nalogi – 2 točki;
1 naloga – 1 točka.

Dobro opravljeno. Vse so dali na stran. Fantje, v naše kartice znanja vpišimo število točk, doseženih za "Matematično bitko" ( Priloga 1).

IV. Predstavitev gradiva

Odprite delovne zvezke. Zapiši številko, odlično delo.

Katere operacije s pozitivnimi in negativnimi števili poznate?
Kako sešteti dve negativni števili?
Kako sešteti dve števili z različnimi predznaki?
Kako odšteti števila z različnimi predznaki?
Vedno uporabljate besedo "modul". Kaj je modul števila? A?

Današnja tema lekcije je povezana tudi z delovanjem števil različnih predznakov. Vendar je bil skrit v anagramu, v katerem morate zamenjati črke in dobiti znano besedo. Poskusimo ugotoviti.

ENOZHEUMNI

Zapišemo temo lekcije: "Množenje."

Namen naše lekcije: seznaniti se z množenjem pozitivnih in negativnih števil ter oblikovati pravila za množenje števil z enakimi in različnimi znaki.

Vsa pozornost na tablo. Pred vami je tabela s problemi, pri reševanju katerih bomo oblikovali pravila za množenje pozitivnih in negativnih števil.

2*3 = 6°C;
–2*3 = –6°С;
–2*(–3) = 6°С;
2*(–3) = –6°С;

1. Temperatura zraka se vsako uro dvigne za 2°C. Zdaj termometer kaže 0°C ( Dodatek 2– termometer) (diapozitiv 1 na računalniku).

Koliko ste prejeli?(6 ° Z).
Nekdo bo rešitev zapisal na tablo, mi pa smo vsi v zvezke.
Poglejmo na termometer, ali smo dobili pravilen odgovor? (diapozitiv 2 na računalniku).

2. Temperatura zraka vsako uro pade za 2°C. Termometer zdaj kaže 0°C (slide 3 na računalniku). Kakšno temperaturo zraka bo pokazal termometer po 3 urah?

Koliko ste prejeli?(–6 ° Z).
Ustrezno rešitev zapišemo na tablo in v zvezke. Analogija s 1. nalogo.
.(diapozitiv 4 na računalniku).

3. Temperatura zraka vsako uro pade za 2°C. Termometer zdaj kaže 0°C (diapozitiv 5 na računalniku).

Koliko ste prejeli?(6 ° Z).
Ustrezno rešitev zapišemo na tablo in v zvezke. Analogija s 1. in 2. nalogo.
Primerjajmo rezultat z odčitkom termometra.(diapozitiv 6 na računalniku).

4. Temperatura zraka se vsako uro dvigne za 2°C. Termometer zdaj kaže 0°C (diapozitiv 7 na računalniku). Kakšno temperaturo zraka je kazal termometer pred 3 urami?

Koliko ste prejeli?(–6 ° Z).
Ustrezno rešitev zapišemo na tablo in v zvezke. Analogija z nalogami 1-3.
Primerjajmo rezultat z odčitkom termometra.(diapozitiv 8 na računalniku).

Poglej svoje rezultate. Pri množenju števil z enakimi predznaki (primera 1 in 3), s katerim predznakom ste dobili odgovor? (pozitivno).

Globa. Toda v primeru 3 sta oba dejavnika negativna, odgovor pa pozitiven. Kateri matematični koncept vam omogoča prehod od negativnih števil k pozitivnim? (modul).

Pravilo pozornosti:Če želite pomnožiti dve števili z enakimi znaki, morate pomnožiti njihove absolutne vrednosti in pred rezultatom postaviti znak plus. (2 osebi ponovita).

Vrnimo se k primeru 3. Čemu sta enaka modula (–2) in (–3)? Pomnožimo te module. Koliko ste prejeli? S kakšnim znakom?

S katerim predznakom ste pri množenju števil z različnimi predznaki (primera 2 in 4) dobili odgovor? (negativno).

Oblikujte svoja pravila za množenje števil z različnimi predznaki.

Pravilo: Ko množite števila z različnimi predznaki, morate pomnožiti njihove module in pred rezultat postaviti znak minus. (2 osebi ponovita).

Vrnimo se k primeru št. 2 in št. 4. Kakšne so velikosti njihovih dejavnikov? Pomnožimo te module. Koliko ste prejeli? Kakšen znak je treba dati kot rezultat?

S tema dvema praviloma lahko tudi množite ulomke: decimalne, mešane, navadne.

Na tabli pred vami je več primerov. Za tri se bomo odločili skupaj z mano, ostale pa sami. Bodite pozorni na snemanje in oblikovanje.

Dobro opravljeno. Odprimo učbenike in označimo pravila, ki se jih moramo naučiti za naslednjo lekcijo (stran 190, §7 (točka 35)). Poznavanje teh pravil vam bo v prihodnosti pomagalo hitro obvladati deljenje pozitivnih in negativnih števil.

V. Matematična veriga

In zdaj Dunno želi preveriti, kako ste se naučili novo snov, in vam bo zastavil nekaj vprašanj. Rešitev in odgovore si obvezno zapišemo v zvezke ( Dodatek 3– matematična veriga).

Računalniška predstavitev
Zdravo družba. Vidim, da ste zelo pametni in radovedni, zato bi vas rad vprašal nekaj vprašanj. Bodite previdni, zlasti pri znakih.
Moje prvo vprašanje je: pomnoži (–3) z (–13).
Drugo vprašanje: pomnoži to, kar si dobil pri prvi nalogi (–0,1).
Tretje vprašanje: rezultat druge naloge pomnožite z (–2).
Četrto vprašanje: pomnoži (-1/3) z rezultatom tretje naloge.
In še zadnje, peto vprašanje: izračunajte zmrzišče živega srebra tako, da rezultat četrte naloge pomnožite s 15.
Hvala za delo. Želim ti uspeh.

Fantje, preverimo, kako smo opravili naloge. Vsi so vstali.

Koliko ste dobili pri prvi nalogi?

Tisti, ki imajo drugačen odgovor, se usedejo, tistim, ki se usedejo, pa si damo 0 točk za matematično verigo na evidenčnem kartončku znanja. Ostali ne dajo ničesar.

Koliko ste dobili pri drugi nalogi?

Tisti, ki imate drugačen odgovor, se usedite in vpišite 1 točko na svoj karton znanja za matematično verigo.

Koliko ste dobili pri tretji nalogi?

Tisti, ki imate drugačen odgovor, se usedite in svojemu kartončku znanja dodajte 2 točki za matematično verigo.

Koliko ste dobili pri četrti nalogi?

Če imate drugačen odgovor, se usedite in svojemu kartončku znanja dodajte 3 točke za matematično verigo.

Koliko ste dobili pri peti nalogi?

Tisti, ki imate drugačen odgovor, se usedite in na svoj karton znanja za matematično verigo vpišite 4 točke. Preostali fantje so pravilno rešili vseh 5 nalog. Sedi, za matematično verigo na kartici znanja si daš 5 točk.

Kakšna je zmrziščna točka živega srebra?(–39 °C).

VI. Domača naloga

§7 (35. člen, stran 190), št. 1121 – učbenik: Matematika. 6. razred: [N.Ya.Vilenkin in drugi]

Ustvarjalna naloga: Napišite nalogo o množenju pozitivnih in negativnih števil.

VII. Test

Preidimo na naslednjo stopnjo lekcije: izvedba testa ( Dodatek 4).

Naloge morate rešiti in obkrožiti številko pravilnega odgovora. Za prvi dve pravilno opravljeni nalogi prejmete 1 točko, za 3. nalogo - 2 točki, za 4. nalogo - 3 točke. Začeli smo z delom.

Δ –1 točka;
o –2 točki;
– 3 točke.

Zdaj pa zapišimo številke pravilnih odgovorov v tabelo pod testom. Preverimo rezultate. V prazne celice bi morali dobiti številko 1418 (pišem na tablo). Kdor ga je prejel, na kartico znanja pripiše 7 točk. Tisti, ki so se zmotili, so na evidenčni kartonček znanja vpisali število doseženih točk samo za pravilno opravljene naloge.

Velika domovinska vojna je trajala natanko 1418 dni, v katerih je ruski narod zmagal za visoko ceno. In 9. maja 2010 bomo praznovali 65. obletnico zmage nad nacistično Nemčijo.

VIII. Povzetek lekcije

Zdaj pa izračunajmo skupno število točk, ki ste jih dosegli pri učni uri, in vnesite rezultate v karton znanja učencev. Nato razdelimo te karte.

15 – 17 točk – ocena »5«;
10 – 14 točk – ocena »4«;
manj kot 10 točk - ocena "3".

Dvignite roke, kdor je prejel "5", "4", "3".

Katero temo smo obravnavali danes?
Kako množiti števila z enakimi predznaki; z različnimi znaki?

Tako se je naša lekcija končala. Želim reči HVALA za vaše delo v tej lekciji.

) in imenovalec za imenovalcem (dobimo imenovalec produkta).

Formula za množenje ulomkov:

Na primer:

Preden začnete množiti števce in imenovalce, morate preveriti, ali je mogoče ulomek zmanjšati. Če lahko ulomek zmanjšate, boste lažje delali nadaljnje izračune.

Deljenje navadnega ulomka z ulomkom.

Deljenje ulomkov z naravnimi števili.

Ni tako strašno, kot se zdi. Tako kot pri seštevanju pretvorimo celo število v ulomek z ena v imenovalcu. Na primer:

Množenje mešanih ulomkov.

Pravila za množenje ulomkov (mešano):

pretvori mešane ulomke v neprave ulomke;
množenje števcev in imenovalcev ulomkov;
zmanjšajte delež;
Če dobimo nepravi ulomek, potem nepravi ulomek pretvorimo v mešani ulomek.

Opomba!Če želite pomnožiti mešani ulomek z drugim mešanim ulomkom, jih morate najprej pretvoriti v obliko nepravih ulomkov, nato pa pomnožiti po pravilu za množenje navadnih ulomkov.

Drugi način množenja ulomka z naravnim številom.

Morda bo bolj priročno uporabiti drugo metodo množenja navadnega ulomka s številom.

Opomba!Če želite ulomek pomnožiti z naravnim številom, morate imenovalec ulomka deliti s tem številom, števec pa pustiti nespremenjen.

Iz zgornjega primera je razvidno, da je ta možnost bolj priročna za uporabo, ko je imenovalec ulomka brez ostanka deljen z naravnim številom.

Večnadstropni ulomki.

V srednji šoli pogosto srečamo trinadstropne (ali več) frakcije. primer:

Če želite tak ulomek prenesti v običajno obliko, uporabite deljenje na 2 točki:

Opomba! Pri deljenju ulomkov je vrstni red deljenja zelo pomemben. Bodite previdni, tukaj se zlahka zmedete.

Opomba, Na primer:

Pri delitvi enega s katerimkoli ulomkom bo rezultat isti ulomek, le obrnjen:

Praktični nasveti za množenje in deljenje ulomkov:

1. Najpomembnejša stvar pri delu z ulomki je natančnost in pozornost. Vse izračune opravite previdno in natančno, zbrano in jasno. Bolje je, da v osnutek napišete nekaj dodatnih vrstic, kot da se izgubite v miselnih izračunih.

2. Pri nalogah z različnimi vrstami ulomkov pojdite na vrsto navadnih ulomkov.

3. Zmanjšujemo vse ulomke, dokler ni več mogoče zmanjševati.

4. Večstopenjske ulomke pretvorimo v navadne z deljenjem na 2 točki.

5. Enoto v glavi razdelite na ulomek, tako da ulomek preprosto obrnete.